In eigentlich allen Vorlesungen zur Analysis trifft man auf Sie – Folgen und ihre Grenzwerte sowie allerlei Abarten wie rekursive Folgen und weiteren Bereichen.
Nur gut, dass man mit WolframAlpha auch diesen Bereich hilfreich beackern kann – hier nun einmal eine Auflistung nützlicher Befehle für Folgen und ihre Anwendung.
Explizite Folgen
- Bildungsvorschrift finden
Auch wenn für diesen Bereich keine allgemeine Theorie existiert (d.h. man kann nicht von allen Folgen eine explizite Bildungsvorschrift angeben), so gibt sich unser Rechenkünstler große Mühe, für eine eingegebene Folge von Zahlen die Bildungsvorschrift zu finden (ganz nach unten scrollen):
Beispiel 1: 1,7,17,31,49
Beispiel 2: 2,3,5,7,11,13,17,19
Selbst das letzte Beispiel erkennt er als Folge der Primzahlen – zwar kann er hier keine Bildungsvorschrift angeben, allerdings gibt er uns dafür die weiteren Folgeglieder.
- Folgeglieder berechnen
Was in die eine Richtung geht, geht natürlich auch anders herum. Gebt ihr eure Folge als Input ein, so erkennt WolframAlpha es als Folge und berechnet davon die ersten Folgeglieder – für den, der zu faul zum Kopfrechnen ist (Was wir natürlich nicht unterstützen…)
Beispiel 1: (3^n+n^2-2)/(n!)
Beispiel 2: (3^n+n^2-2)/(n!)
Am Anfang bekommt ihr Bilder zur Folge, die könnt ihr ignorieren. Danach kommt der Bereich Values – mit einem Klick rechts auf more, macht er genau das, was man vermutet: er berechnet weitere Folgeglieder.
- Grenzwerte berechnen
Die Grenzwertbetrachtung für Folgen ist analog der für Funktionen – die Schlagwörter die man sich einprägen muss sind limes sowie +/- infinity
Beispiel 1: limes n to infinity (5^n-3^n)/(5^(n+1)-3^(n+1))
Beispiel 2: limes n to infinity sqrt(n+1) - sqrt(n)
Beispiel 3: limes n to infinity (e^(-n)/n)
Man hat sogar das Glück, dass man rechts auf show steps sich die einzelnen Rechenschritte anzeigen lassen kann – leider funktioniert das nicht bei allen Folgen, wie man an dem oberen Beispiel 1 sehen kann.
Und wenn es keinen Grenzwert gibt?
Auch dieses Ergebnisses wird uns ausgegeben – allerdings nicht offentsichtlich, wie wir an diesem Beispiel sehen werden:
Beispiel: limes n to infinity (-1)^n
Diese Folge ist alternierend zwischen den Werten 1 und -1, d.h. sie besitzt keinen eindeutigen Grenzwert. WolframAlpha spuckt uns allerdings ein Ergebnis aus:
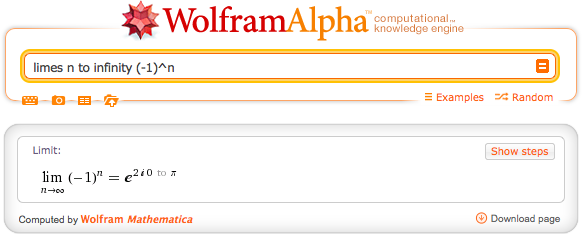
Wer hier nur Bahnhof versteht – keine Angst. Wenn ihr ein Ergebnis mit
„e hoch 2i 0 to pi“
bekommt, so bedeutet das: es gibt keinen Grenzwert! Warum WolframAlpha hier als Ergebnis den Kreis mit den Häufungspunkten der Folge angibt (in komplexer Schreibweise!), wissen wir selbst nicht genau – da sollte man mal wirklich nachfragen. :)
Rekursive Folgen
Auch bei rekursiven Folgen wird man nicht entäuscht, wenngleich hier die Möglichkeiten für Berechnungen nicht so groß sind. Zumindest kann man eine rekursive Folge mit Startglied angeben und es wird, wenn möglich, eine explizite Vorschrift gefunden. Hat man diese, kann man dann mit den Befehlen von oben weitermachen.
Beispiel: solve a(n+1)=1+2a(n), a(0)=1
Dabei benutzt ihr das Codewort solve und gebt eure rekursive Bildungsvorschrift sowie eurer Startglied per Komma getrennt an – fertig!
Was, mehr geht nicht?
Auch wenn es schade ist – wirklich mehr kann man noch nicht abfragen. Natürlich kriegt man mit einigem Aufwand durch die Befehle supremum, infimum ein Gefühl für die Beschränktheit, allerdings nur mit erheblicher Tüftelei und ohne einen Befehl, der alles macht. Eine komplette Übersicht der Befehle für Folgen findest du hier.
Genau wie in der Mathematik helfen euch diese Befehle auch für den Bereich der Reihen. Im nächsten Tutorial werden wir deswegen auf Befehle für Summen und Reihen eingehen!

